[Data_Structer] 기초자료구조 정리

Array & LinkedList

우선 자료구조의 기본이라고 할 수 있는 Array 에 대해서 보자. Array는 논리적 순서와 물리적 순서가 일치한다. 따라서 index값을 통한 원소 접근이 용이하며, 구현이 쉽다. 단점으로는 삽입, 삭제 등에 대한 연산에 필요한 Cost가 높다는 것이다. 삭제의 경우 순서를 맞추기 위해, 뒤의 원소들을 모두 앞으로 Shift연산을 해줘야 하며, 삽입의 경우도 삽입한 인덱스 포함, 그 뒤의 인덱스들에 Shift 연산을 해줘야 한다.

배열의 삽입/삭제 연산에 대한 비효율성을 극복하고자 등장한 것이 LinkedList 이다.

Array와 LinkedList의 차이점은, Array는 논리적, 물리적 저장이 순서대로 되어있으나, LinkedList는 논리적으론 순서대로 되어있으나 물리적으론 순서대로 되어있지 않다.

대신 LinkedList는 각 원소가 다음 index 위치에 해당하는 물리적 주소를 가지고 있다. 그렇기에 삽입/삭제시에는 데이터를 Shift할 필요 없이, 해당되는 원소의 물리적 주소만 변경해주면 된다.

하지만 이 같은 특징 때문에 원하는 index를 참조하려면, 1번 index부터 차례대로 접근해야 한다는 비효율성이 있다.

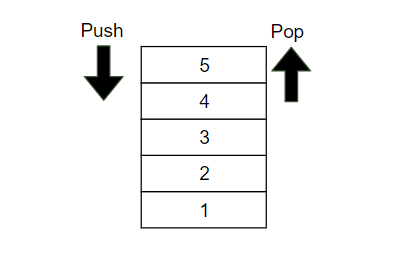
Stack & Queue

Stack 은 선형 자료구조의 일종으로, FILO(First In Last Out)의 대표적인 예시로 들 수 있으며, 말 그대로 먼저 들어갔다가 나중에 나오는 구조이다. 즉 가장 나중에 들어간 원소가 가장 먼저 나오게 된다. 미로찾기, 괄호 유효성 체크 등에 활용된다.

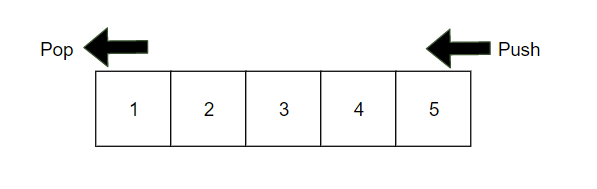
Queue 역시 선형 자료구조이며, Stack과는 반대로 FIFO(First In First Out) 구조이다. 줄을 선다는 뜻과 같게, 먼저 들어간 원소가 가장 먼저 나온다. 작업 우선순위, Heap 구현 등에 사용된다.

Tree

Tree 는 Stack, Queue와는 다르게 비선형 자료구조로, 계층적 구조를 표현하는 자료구조이다. 실제 데이터를 삽입하고 삭제한다는 생각 이전에, 표현에 집중하자. 트리의 구성 요소는 다음과 같다.

• Node (노드) : 트리를 구성하고 있는 원소 그 자체를 말한다.
• Edge (간선) : 노드와 노드사이를 연결하고 있는 선을 말한다.
• Root(Node) : 트리에서 최상위 노드를 말한다.
• Terminal(Node) : 트리에서 최하위 노드를 말한다. Leaf Node라고도 한다.
• Internal(Node) : 트리에서 최하위 노드를 제외한 모든 노드를 말한다.

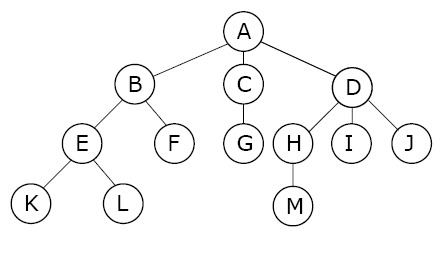
Binary Tree (이진트리)

Binary Tree는 Root 노드를 포함, Leaf 노드를 제외한 모든 노드의 자식이 두 개인 것을 말한다. 공집합 역시 노드로 인정한다. 노드로 이루어진 각 층을 Level이라 하며, Level의 수를 이 트리의 height라 한다.

이진트리에는 모든 Level이 가득 찬 이진 트리인 Full Binary Tree(포화 이진 트리) 와 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워진 트리인 Complete Binary Tree(완전 이진 트리) 가 있다(두 트리의 차이점을 알아두면 좋을 것 같다). 배열로 포화 이진트리와 완전 이진트리를 구현했을 때, 노드의 개수 n에 대해서 i번째 노드에 대해서 parent(i) = i/2 , left_child = 2i, right_child = 2i + 1 의 인덱스 값을 갖는다.

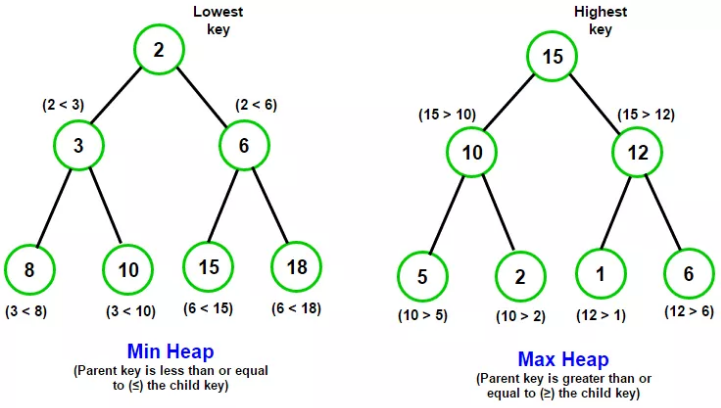
Binary Heap

Binary Heap은 배열에 기반한 완전 이진탐색트리이며, Max-Heap과 Min-Heap이 있다. Max-Heap은 상위 노드의 값이 하위 각 노드의 값보다 크며, Min-Heap은 반대로 상위 노드의 값이 하위 각 노드의 값보다 작다(형제 노드끼리는 상관없다). 이 성질을 이용하면 최대, 최솟값을 찾아내는 것이 훨씬 용이하다.

HashTable

HashTable은 내부적으로 배열을 사용하며, 평균적으로 빠른 탐색속도(O(1))를 갖는다. 평균적으로라는 의미는 충돌을 고려하지 않았을 때이다. Key값을 해시함수를 통하여 인덱스로 변환 후에, 그 인덱스에 집어 넣는다. 만약 다른 Key값을 해시함수를 통과시켰는데 같은 인덱스가 나온다면, 그걸 충돌이라고 한다. 충돌 해소법(Resolve Conflict) 방법에는 기본적인 두 가지 방법이 있다.

Open Address 방식 (개방 주소법)

충돌 발생 시, 다른 인덱스를 찾는다. Linear Probing : 순차적으로 탐색하여 다음 인덱스를 찾는다. Quadratic Probing : 2차 함수를 이용해 탐색할 위치를 찾는다. Double Hashing Probing : 충돌 발생시 새로운 해시함수를 활용하여 주소를 찾는다.

Separate Chaining 방식 (분리 연결법)

충돌 발생 시 다른 인덱스를 찾는 대신, 그 인덱스에다가 연결하는 방법. 연결 리스트를 이용하여 연결하는 방법과, Tree(RBT)를 이용하여 연결하는 방법이 있다. 두 방식 모두 Worst Case가 O(M)이다. 데이터의 크기가 크다면 Separate Chaining, 아니라면 Open Address 방식이 더 낫다. Hashmap의 Resize : 일정 개수이상 크기가 커지면, 해시 버킷의 크기를 두 배로 늘림.

Graph

정점과 간선의 집합이며, 일종의 Tree이다.

Undirected와 Directed Graph가 있는데, 방향성 유무로 결정된다.

Degree란 Undirectd Graph에서 정점에 연결된 간선의 개수이다. Directed Graph에서의 Degree는 방향성이 있기 때문에 둘로 나뉘는데, 나가는 간선의 개수는 Outdegree, 들어오는 간선의 개수를 Indegree라 한다.

가중치 그래프 란 간선에 가중치를 둔 그래프, 부분 그래프 란 한 그래프의 일부 정점 및 간선으로 이루어진 그래프.

그래프의 구현 방법 :

• 인접 행렬 : 정방 행렬을 사용하여 구현. 연결 관계를 O(1)로 파악 가능. 공간 복잡도는 O(2V)
• 인접 리스트 : 리스트를 사용하여 구현. 정점간 연결 여부 파악애 오래 걸림. 공간 복잡도는 O(E + V)

탐색 방법에는 깊이 우선 탐색(DFS, Depth First Search)와 너비 우선 탐색(BFS, Breadth First Search)이 있다.

깊이 우선 탐색은 말 그대로 깊숙히 들어가서 탐색하고 나오는 것이며, 유용한 자료구조는 Stack이다.

너비 우선 탐색은 임의의 한 정점에 대해 인접한 정점을 queue에 넣고(enqueue), dequeue연산에서 나온 하나의 정점으로 들어가서 그 정점의 인접한 정점을 다시 Queue에 넣어서 탐색하는 방식. BFS로 찾은 경로는 최단 경로이다.