[Coding_Test] Two_Sum 문제풀이

Two Sum 문제

n개의 정수가 저장되어 있는 배열이 하나 주어진다. 배열의 원소를 두 개 더해서 target number가 될 수 있다면 True, 불가하면 False를 반환해라

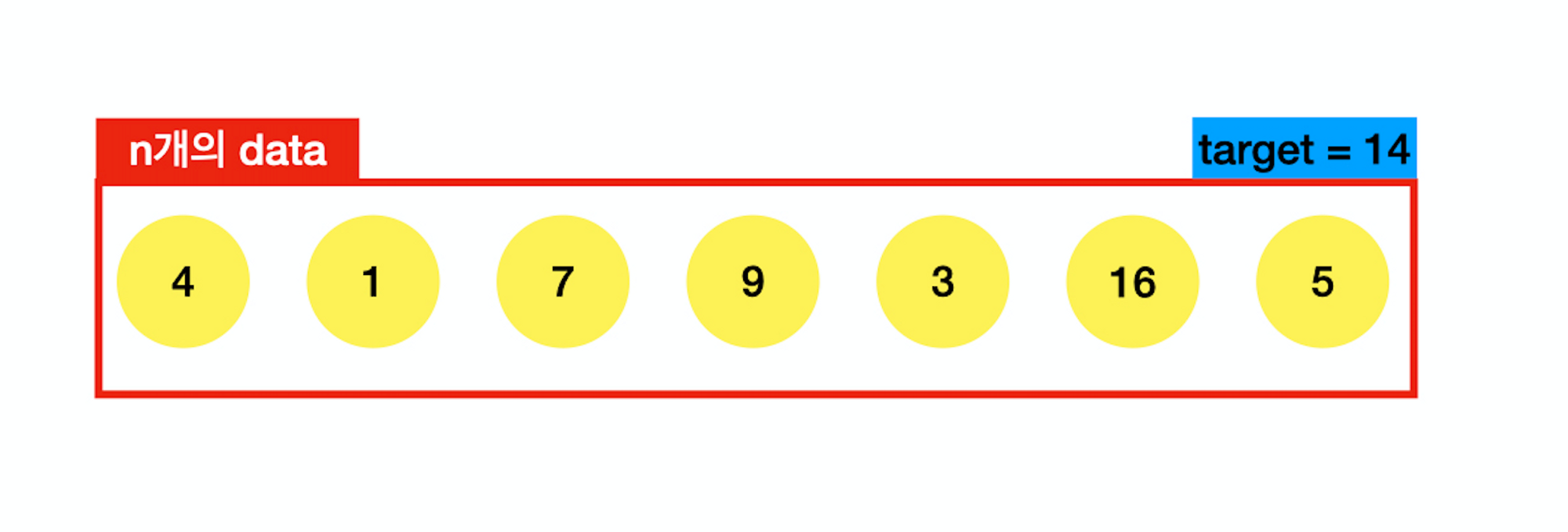
풀이 방법

1. 완전탐색(Brute-force)

   가장 직관적인 풀이 방법은 완전탐색 완전탐색은 간단히 말씀드리면 “무식하게 일일이 다 해보기”

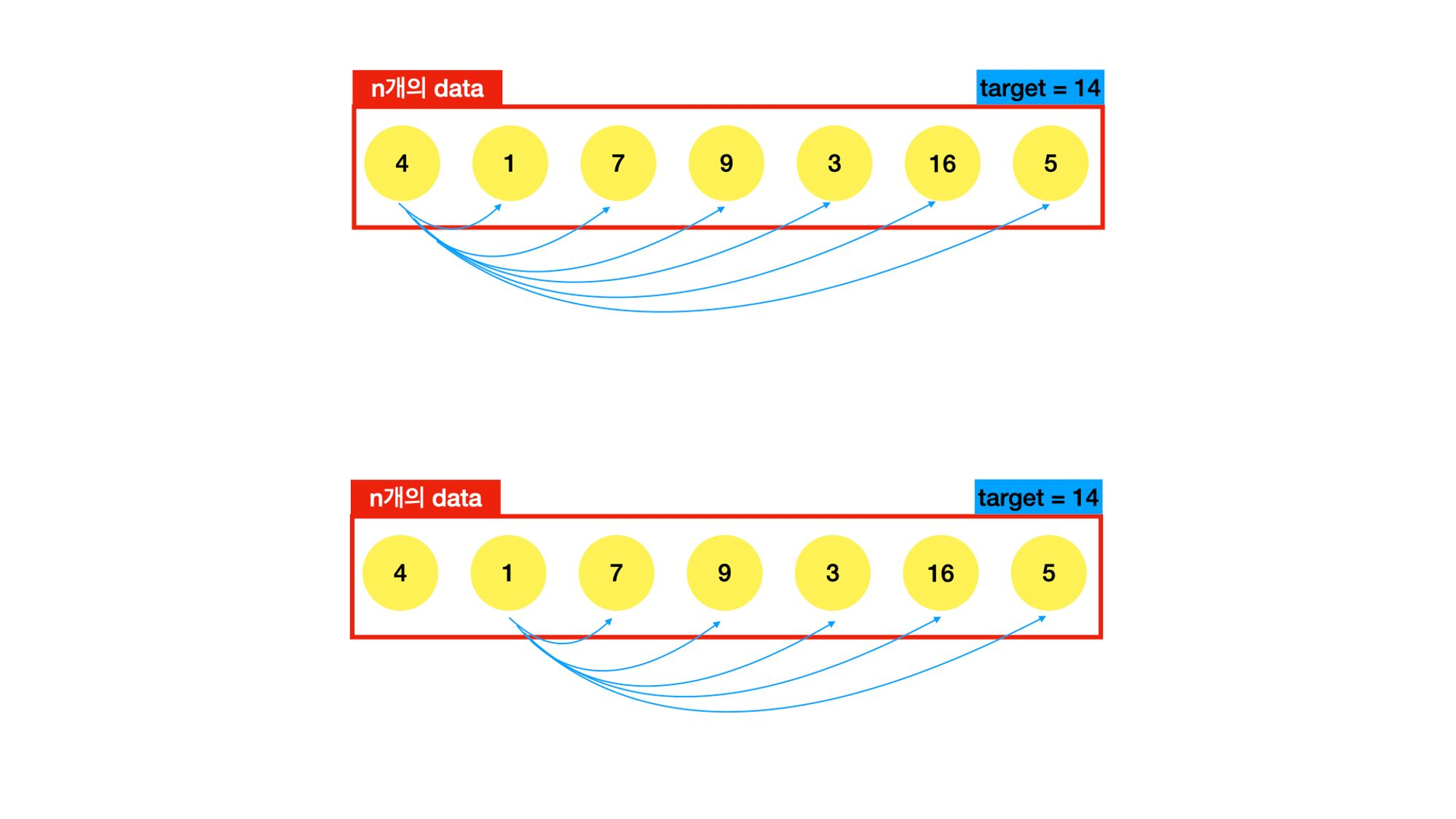
   첫 번째 원소를 선택해서 다른 원소들과 일일이 더해보자. target = 14와 동일한 값이 나오면 True를 반환

   첫 번째 원소에 대해서 일일이 다 해봤으면, 두 번째 원소에 대해서 일일이 해보자. 이 과정을 반복

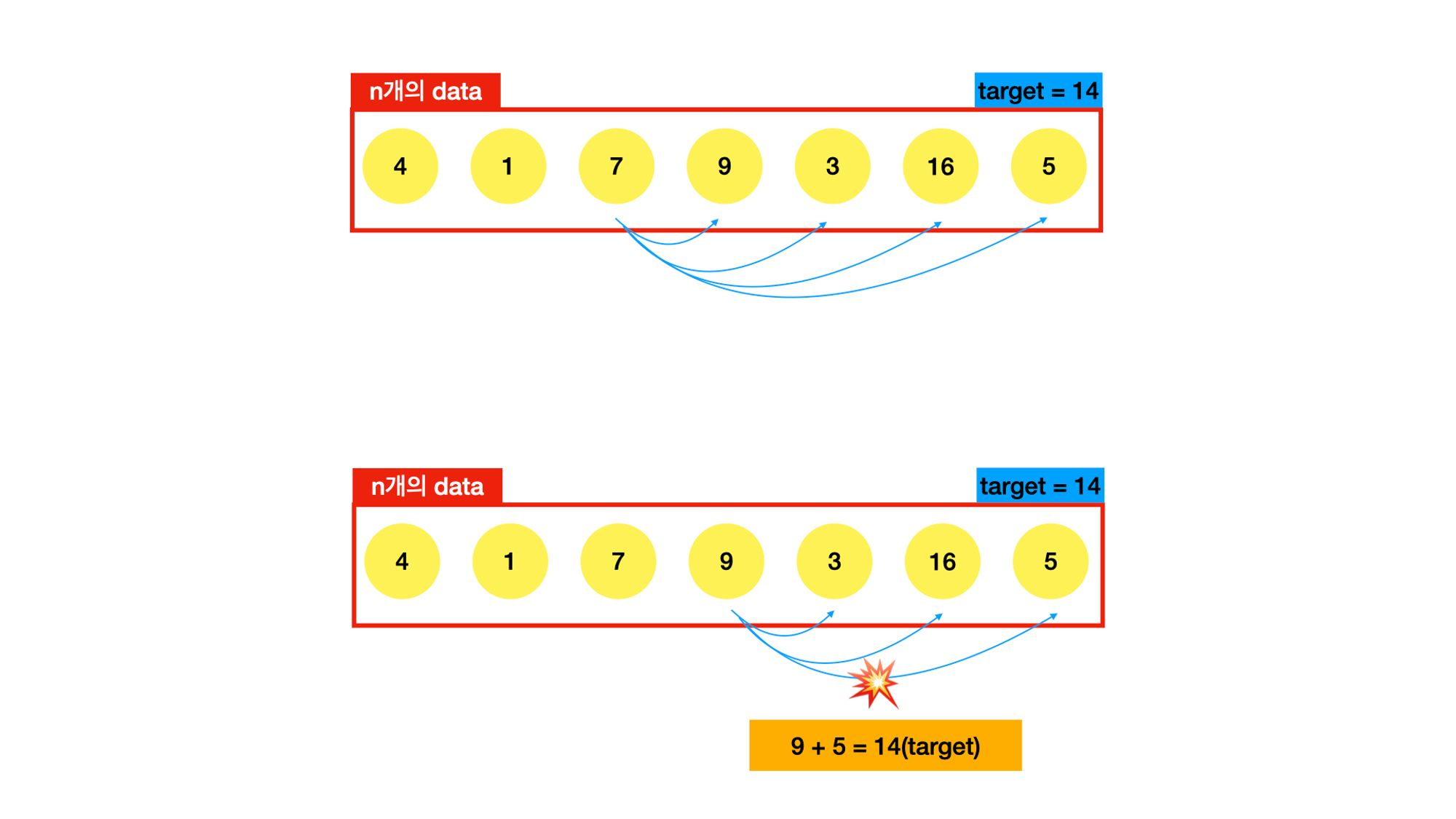
4번째 원소 9와 7번째 원소 5를 더했을 때 14가 나오면, True를 반환

코드로 작성

def twoSum(nums, target):
    for i in range(len(nums)):
        for j in range(i+1, len(nums)):
            if nums[i] + nums[j] == target:
                return [i, j];

시간복잡도는 O(n^2)이고, 여기서 n은 nums 배열의 size

즉 nums 배열의 크기 $n$이 커지면 실행시간은 n^2의 크기로 커진다.

1. 정렬

   데이터를 정렬시키면 좀 더 효율적인 알고리즘을 구상할 수 있는 경우가 종종 있다. sort(), heap, binary search 등을 이용하면 좀 더 효율적인 알고리즘으로 해결할 수 있는지 생각해보자

   이 문제는 정렬을 하면 완전탐색O(n^2) 보다 효율적인 알고리즘으로 풀이를 할 수 있다.

   

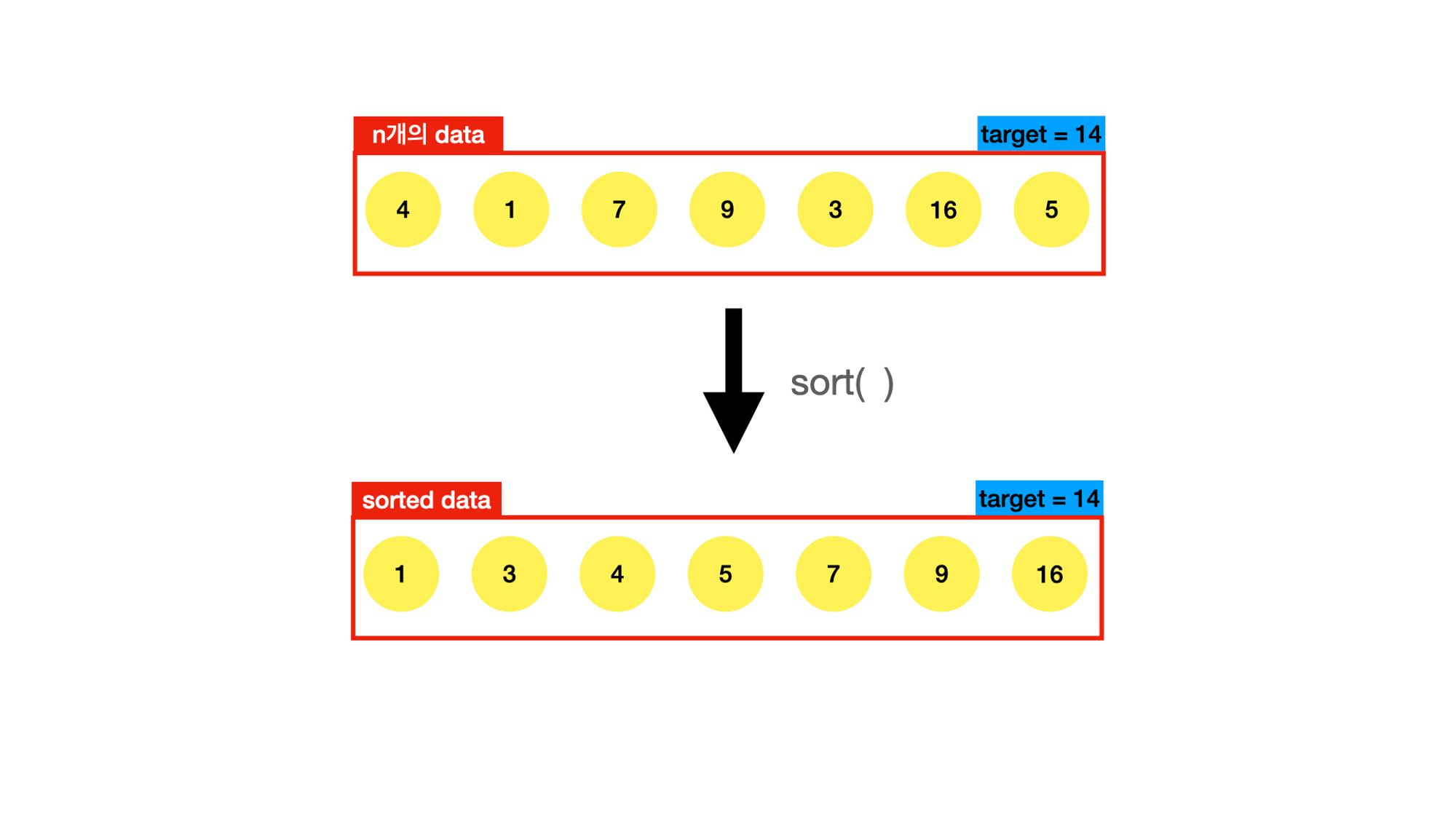
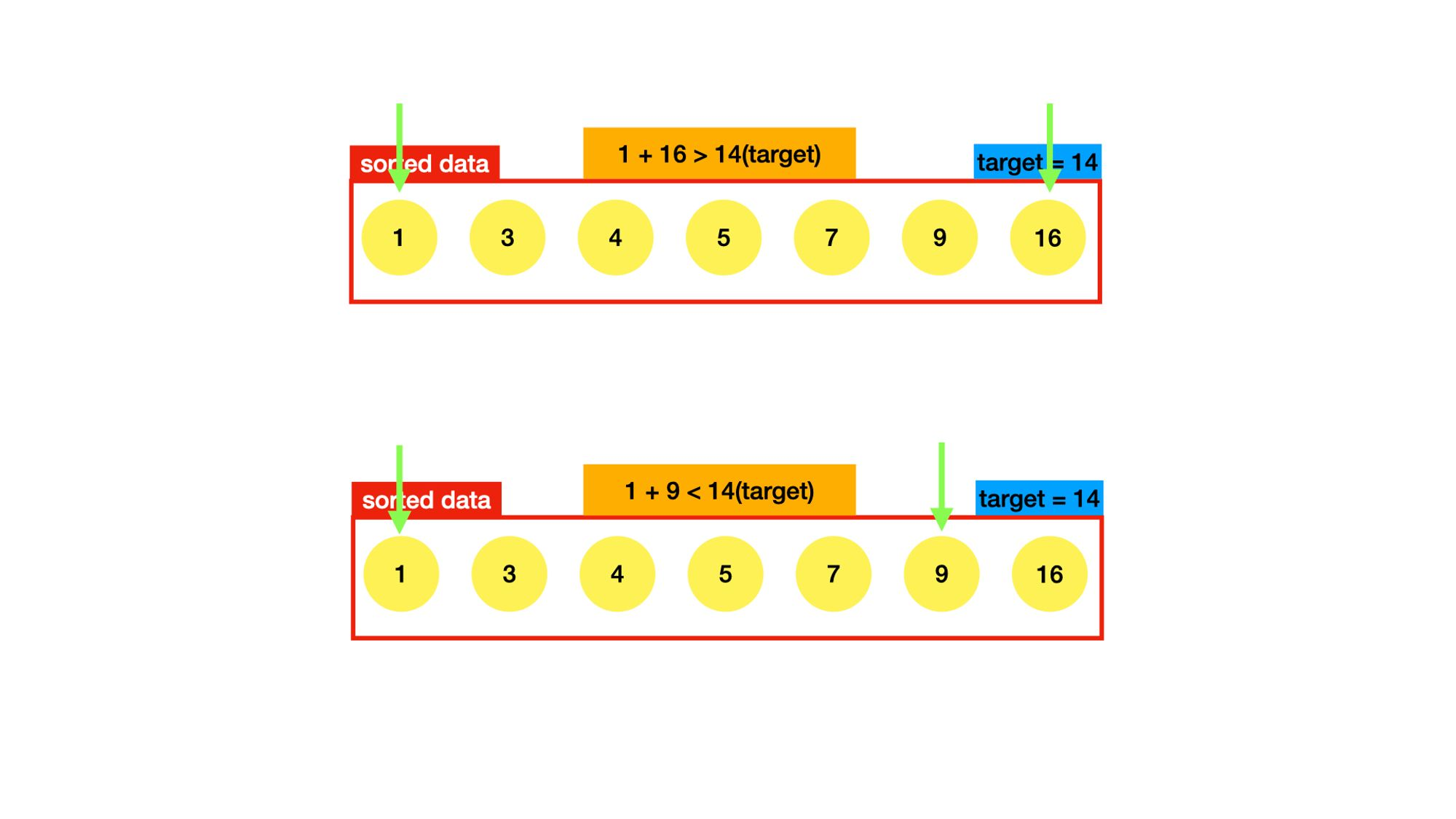
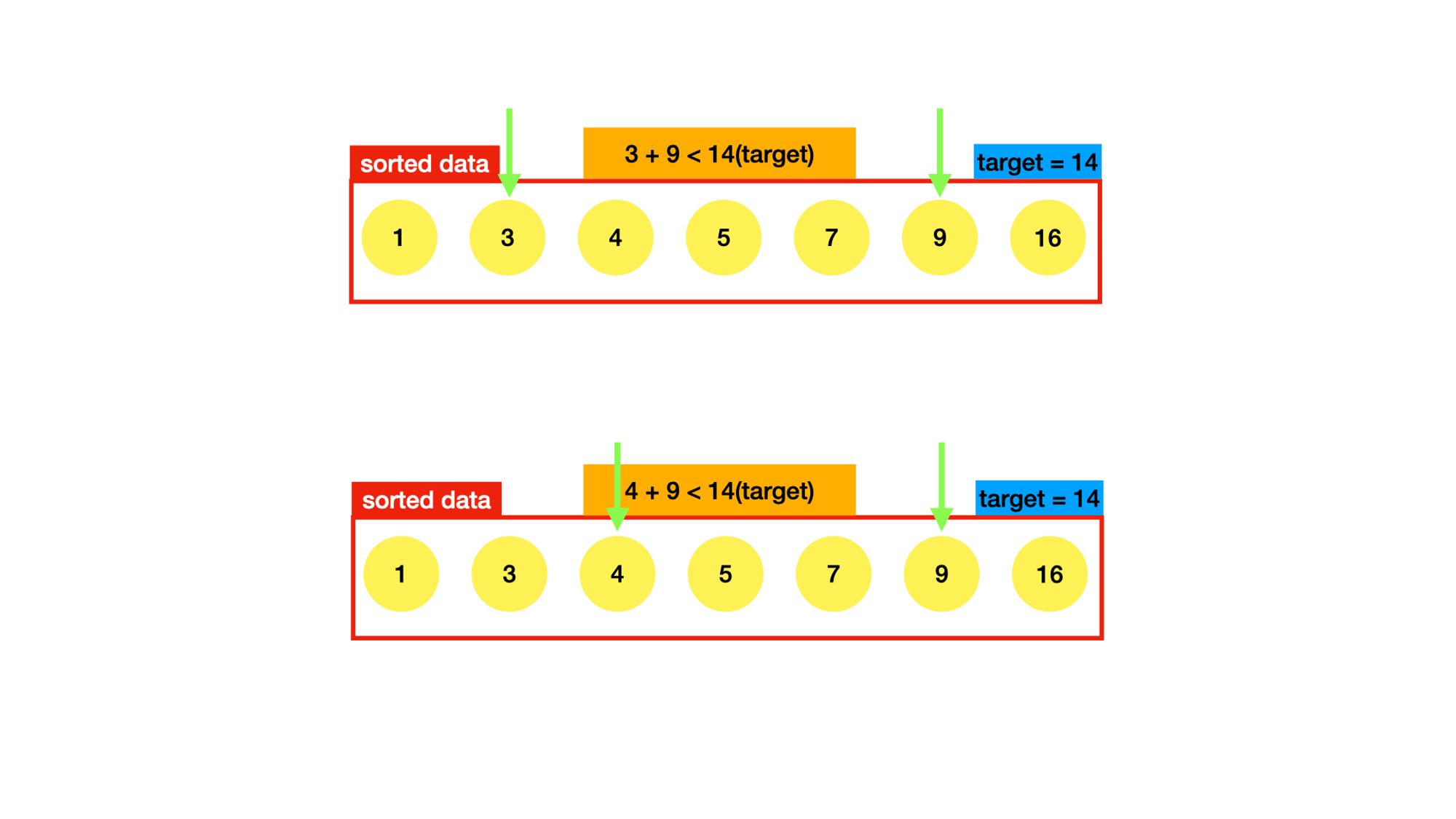
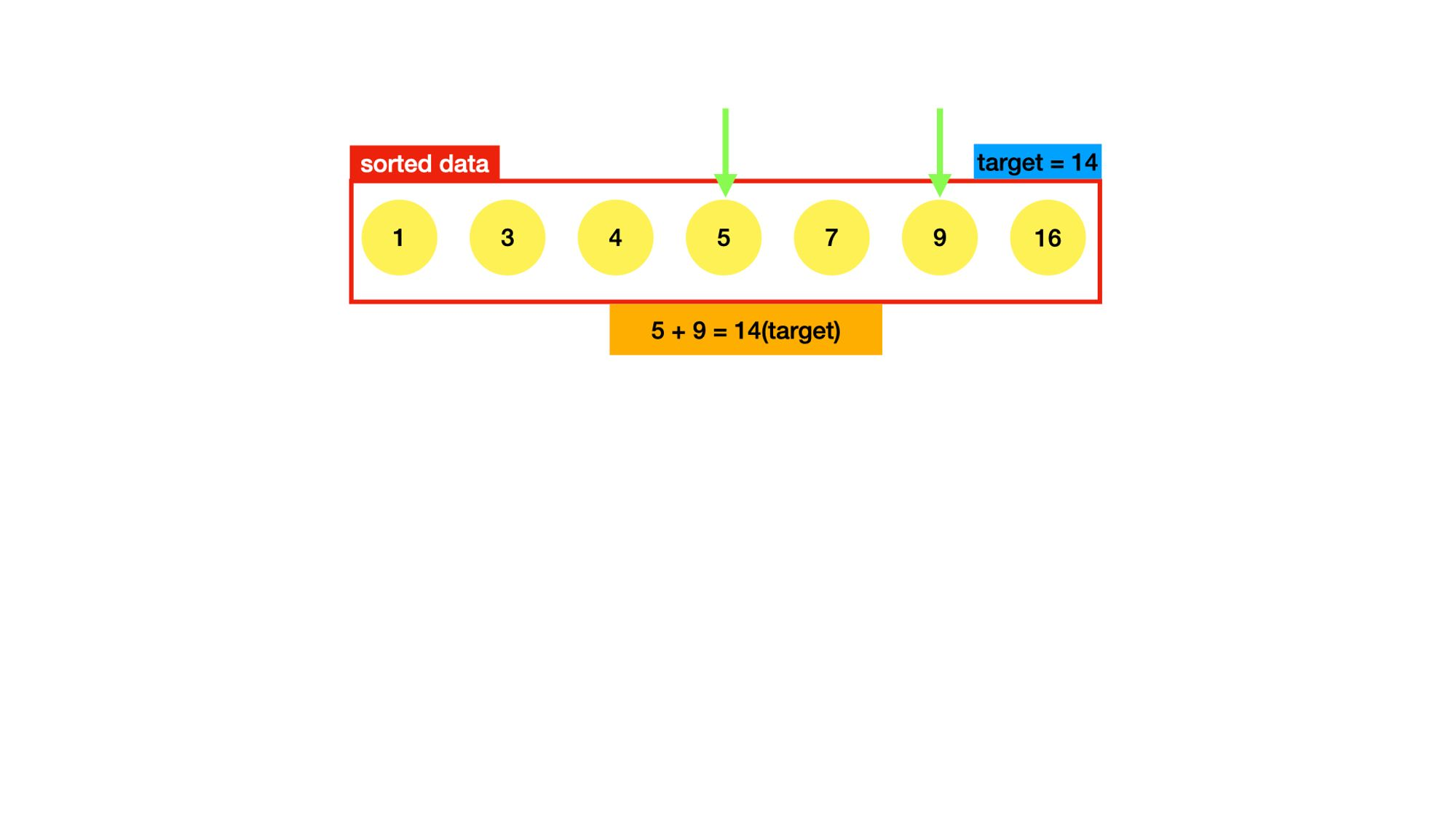
위의 알고리즘은 정렬된 데이터를 이용하는 것이다. 제일 먼저 정렬을 하기위해 sort()메서드 를 사용했다.

⇒ O(nlogn)

정렬된 데이터의 양 끝 index에 있는 두 숫자를 더한 값이 target보다 크면 오른쪽 index를 한 칸 왼쪽으로 옮기고, target보다 작으면 왼쪽 index를 한 칸 오른쪽으로 옮긴다. 이를 target과 같아질 때까지 반복한다.

⇒ O(n)

코드작성

'''
정렬 O(nlogn)
'''
def twoSum(nums, target):
		# O(nlogn)
    nums.sort()

		l, r = 0, len(nums)-1

		# O(n)
		while l < r:
				if target > nums[l] + nums[r] : 
                	l += 1
				elif target < nums[l] + nums[r] : 
                	r -= 1
				else: return True

		return False
				

이 알고리즘의 시간복잡도는 O(nlogn)이다. 부분부분 시간복잡도를 구하더라도, 전체적인 시간복잡도는 가장 차수가 높은 시간복잡도에 맞춰진다(Big-O notation)

이렇게 정렬을 활용하여 완전탐색보다 효율적으로 문제를 풀 수 있었다. 알고리즘 문제를 풀다보면 O(n^2)과 O(nlogn)이 굉장히 큰 차이라는 것을 알게 될 것이다.

1. 메모리를 사용하여 시간효율을 극대화!

   메모리를 잘 사용하면 시간효율을 높일 수 있다. 메모리를 잘 활용한다는 것은 자료구조를 적재적소에 사용한다는 것이다. 배열로 들어온 데이터를 트리나 그래프등으로 변환한 후 문제를 푸는 방식도 있을 것이다. 그 중에서도 가장 자주 사용되고 효과가 굉장히 좋은 것은 hashmap을 사용하는 것이다.

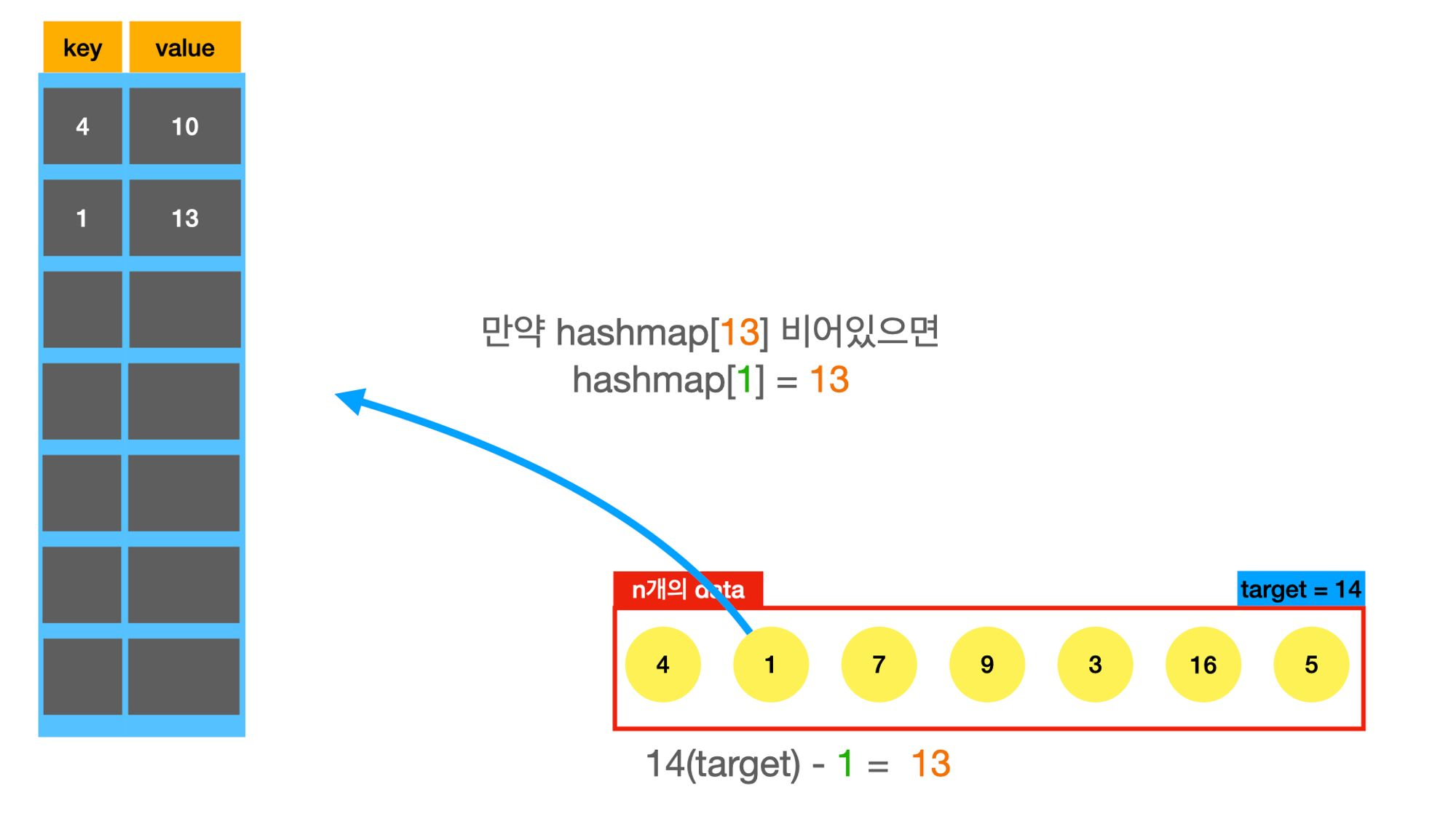
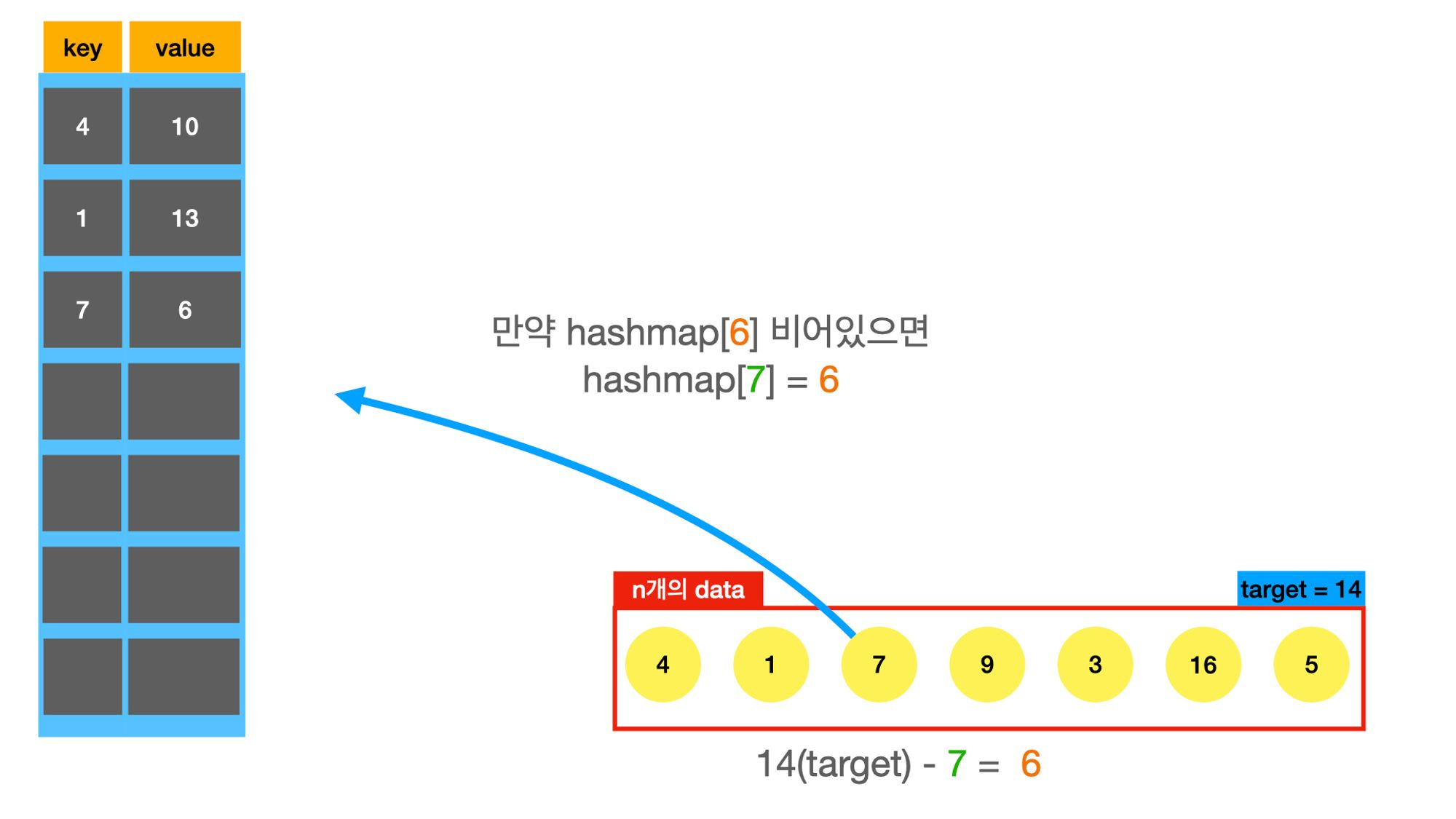
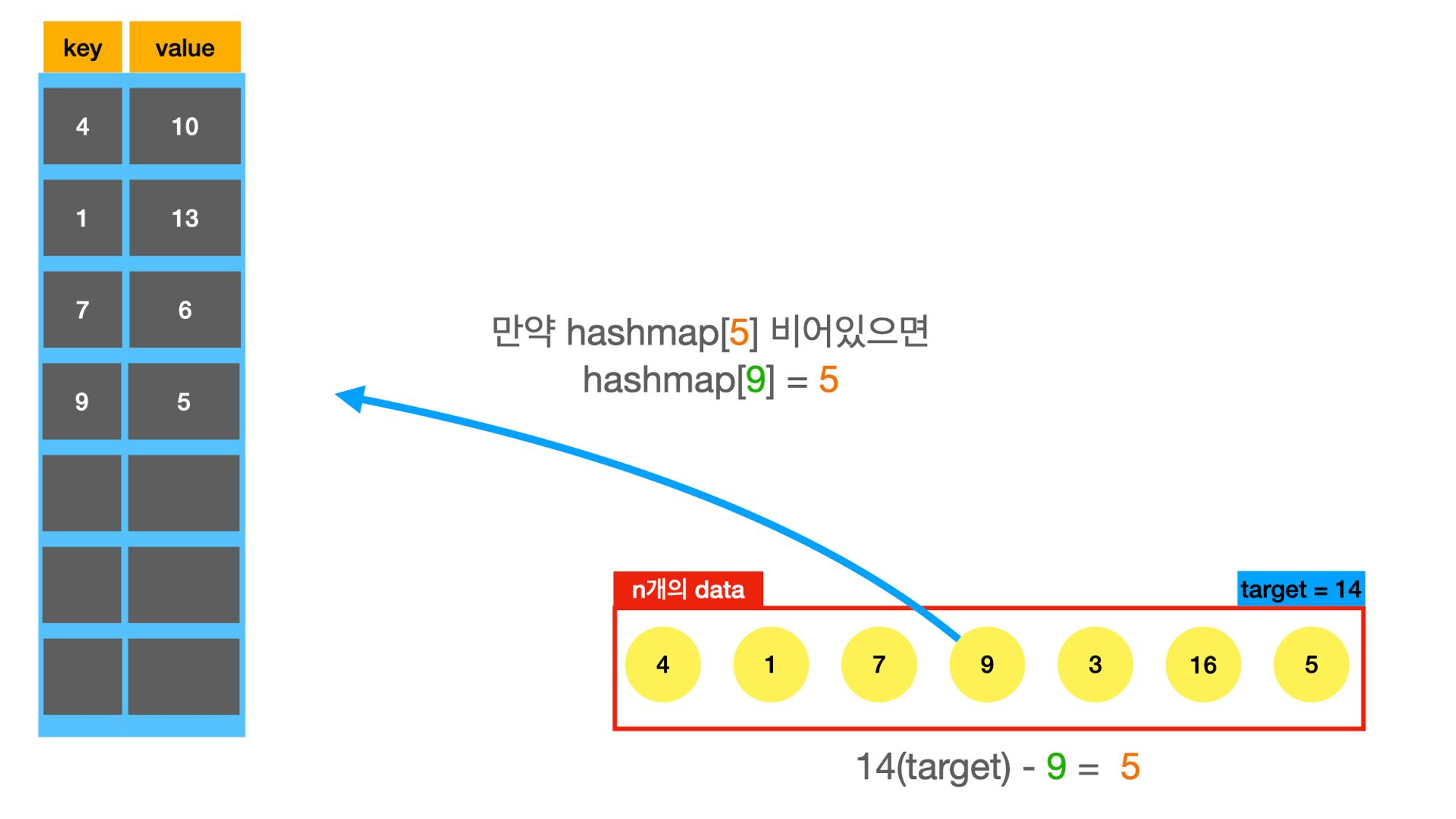
   twosum문제도 hashmap을 적용해보자.

   

'''
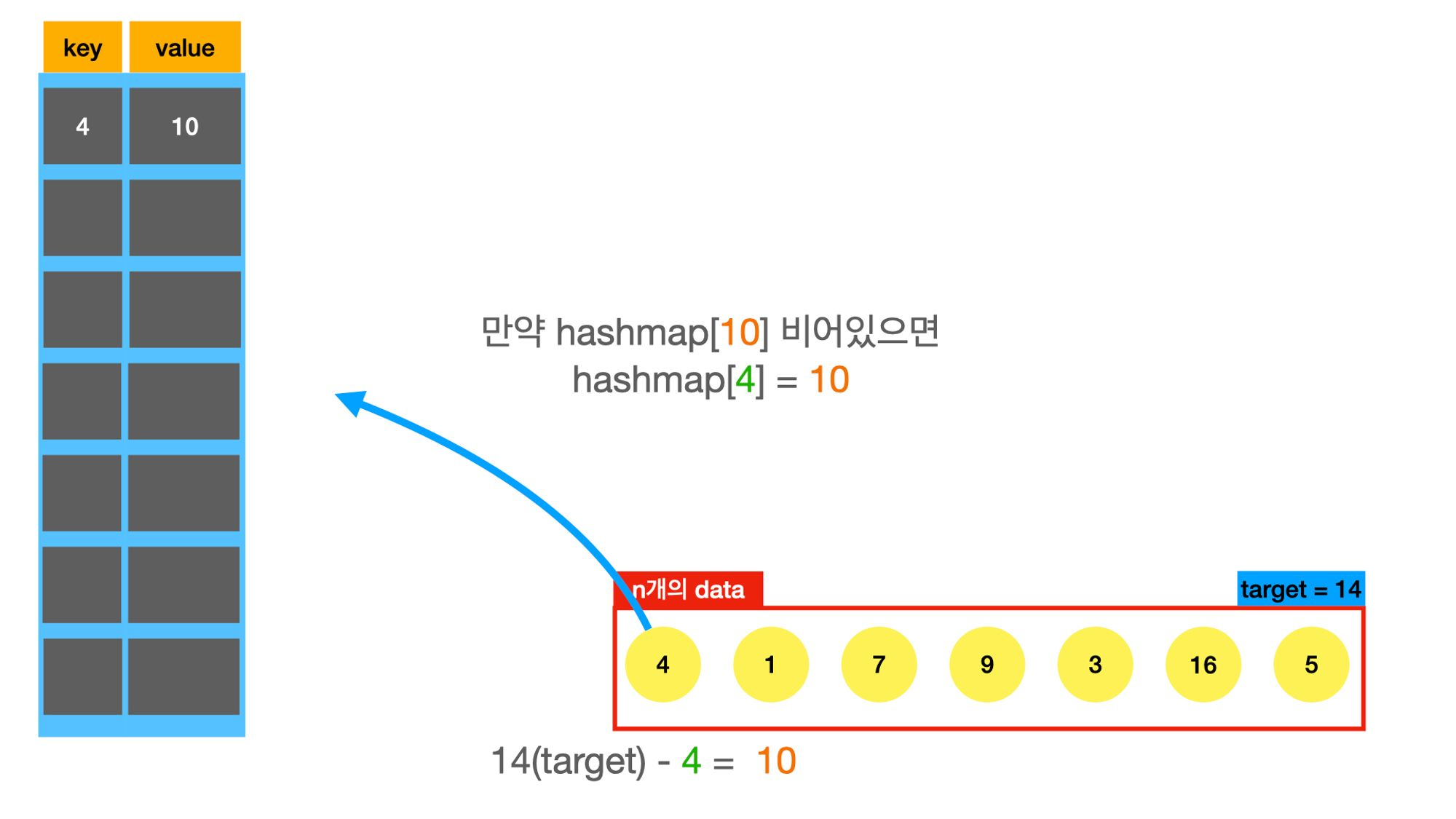
hashmap 이용 O(n)
'''
def two_sum(nums, target):
    memo = {}
    for v in nums:
        memo[v] = True

    for v in nums:
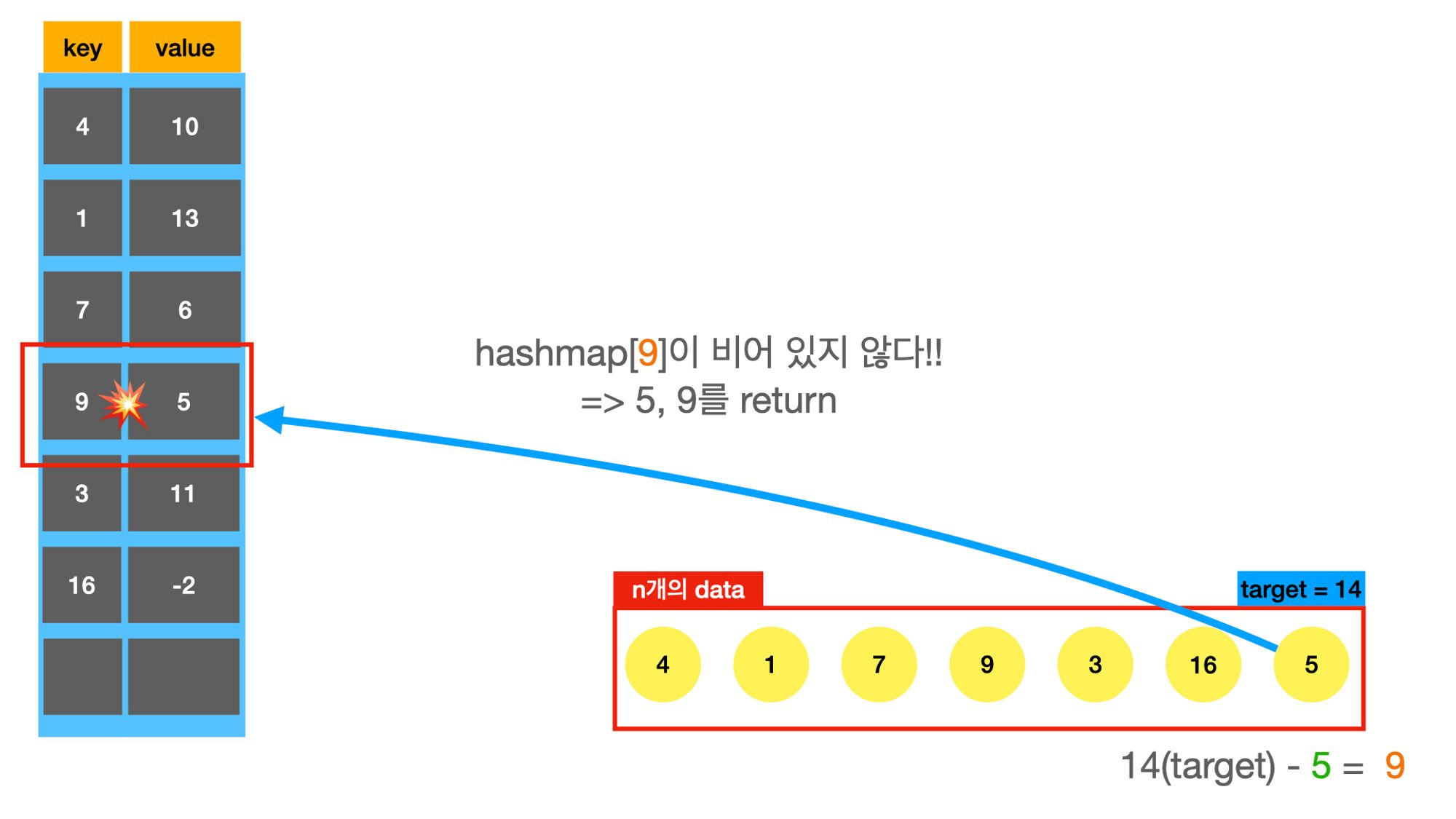
        needed_number = target - v
        if needed_number in memo:
            return True
    return False

print(two_sum([4,1,9,7,5,3,16], 14))

hashmap은 O(1)로 접근할 수 있기 때문에, 메모리가 충분하고 hashmap을 만드는데 시간이 오래걸리지 않으면 굉장히 강력한 도구가 된다. 보통 n개의 데이터로 hashmap을 만들어야 하기 때문에 만드는 과정에서 O(n)의 시간이 든다.

위의 풀이에서도 반복문O(n)을 한번 돌면서 모든 과정을 마쳤다. 따라서 시간복잡도는 O(n)이다.

참조 : 개발남노씨 자료구조